insegnare regole o matematica?

... la matematica è più di una tecnica, è un comportamento ...

INTRO

Lo studio dei fattori nonintellective (Aiken, 1961) nasce nel contesto dell’analisi delle difficoltà che incontrano gli studenti nello studio della matematica e delle possibili azioni di recupero; le modalità tradizionali di osservazione e intervento sono sempre state contestualizzate in ambito puramente cognitivo, interpretando la difficoltà come mancanza di conoscenza. Questa spiegazione presenta però dei limiti, infatti molte delle operazioni di recupero risultano essere inefficaci.
La matematica è una disciplina autonoma affidata a matematici e non a esperti dell’ educazione. Sono diverse e complesse le modalità che mettono in moto le rappresentazioni  dell’allievo  in  situazioni  di  apprendimento dei saperi, degli  strumenti, del funzionamento della classe e delle metodologie didattiche e relazionali, della funzione e del ruolo dell’insegnante. Si tratta di prendere in considerazione tutti quegli aspetti del pensiero umano che non riguardano la pura cognizione, quali ad esempio le emozioni, le convinzioni, l’atteggiamento, il
valore, la motivazione, i sentimenti e gli obiettivi. Questi aspetti vengono quindi introdotti dai ricercatori in didattica della matematica per fornire un’interpretazione alternativa delle difficoltà nella disciplina.

STRUMENTI

* Elementi di didattica della matematica di Bruno D'Amore
* Research on affect in mathematics education: a reconceptualization di
McLeod (1992).
* Self-report

STRATEGIE

* Problemi situati di real life
* Peer education 
* Gamification
* Design didattico
* Team work
* Laboratorio

DESCRIZIONE

A volte ingenuamente pensiamo che quel che noi insegniamo coincida con ciò che la persona che abbiamo di fronte sta imparando, ovviamente non è così. Abbiamo di fronte n persone con n maggiore di 1 e ciascuno sta imparando a modo suo. 
Usare uno strumento, una sola metodologia in aula è già di per sé sinonimo di fallimento perché si raggiungono solo alcuni studenti. Inoltre, non è lo strumento in sé che risolve il problema ma la relazione tra insegnante e allievo: l'apprendimento dell'essere umano è sempre situato. 
In una situazione d'aula noi distinguiamo tre elementi fondamentali: l'allievo, il maestro e il sapere; in questa situazione lo studente interpreta le domande e il linguaggio della matematica non è mai univoco, né mono semantico. Se lo studente vi sembra "non avere logica", "non essere portato", "non capire la materia", provate a osservarlo giocare ai videogames! 
Semplicemente l'interpretazione che lo studente dà a volte della situazione non coincide con quella che ha in mente l'insegnante. La sua vera domanda diventa: ma che cosa devo rispondere per raggiungere il minimo risultato utile? Lo studente cambia mestiere: invece di fare il mestiere di chi apprende la matematica fa il mestiere di chi cerca di capire che cosa vuole l'insegnante. 
Per impegnarsi nel proprio studio e percepire la materia come utile, gli studenti hanno bisogno di avere successo in matematica e di attribuire i buoni risultati ottenuti alle proprie abilità e all’impegno profuso (Alschuler, 1969). Naturalmente le convinzioni riguardo a cos’è il successo in matematica è qualcosa di estremamente soggettivo ed è un fattore fortemente influenzato dalla visione della materia che si possiede. 

MOTIVAZIONE

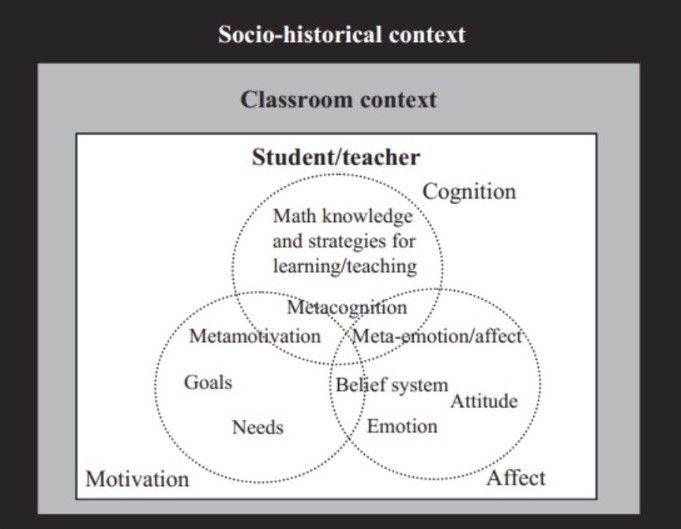
Le tre principali categorie concettuali identificate nel processo di apprendimento sono la cognizione, la motivazione e le emozioni:
• la cognizione tratta con le informazioni riguardo al sé e all’ambiente,
• la motivazione dirige i comportamenti (obiettivi e scelte),
• le emozioni sono la conseguenza dei successi/fallimenti dei comportamenti guidati dai propri obiettivi e attivano un sistema di feedback per i processi cognitivi e motivazionali.
La motivazione in matematica viene sviluppata presto (non più tardi dei 12-13 anni) e diventa stabile nel tempo, poiché viene internalizzata nel concetto di sé. Gli studenti con un concetto di sé basso nei confronti della disciplina devono tale risultato a una serie di brutte esperienze che li hanno portati a cercare di evitare l’ansia che provano quando devo applicarsi su di essa.
Tale processo può essere influenzato dal docente che mostrandosi paziente, incoraggiante, e a supporto dello stile individuale di apprendimento potrebbe far sentire gli studenti a proprio agio, attenuando la preoccupazione di essere umiliati e criticati nel caso in cui vengano commessi errori (Brophy, 1987).
Dovremmo passare da una didattica che studia i programmi, che studia gli strumenti a una didattica che guarda l'aula, guarda gli esseri umani, guarda come i ragazzi e le ragazze interpretano quello gli diciamo. 
Dagli anni sessanta tali lacune furono colmate dalle successive teorie delle motivazioni intrinseche, in concomitanza con l’enfasi sull’apprendimento per scoperta (Bruner, 1961) e sul problem solving. La conseguenza fu una focalizzazione sugli aspetti motivazionali relativi all’attivazione del comportamento esplorativo ed epistemico, ponendo l’accento sul bisogno di imparare e conoscere l’ambiente circostante. Lo scopo dell’istruzione diventa quindi quello di stimolare la curiosità per lo sviluppo della competenza. 
La cognitive evaluation theory non si concentra solo sulle cause della motivazione intrinseca, ma piuttosto sulle condizioni (fattori sociali e ambientali) che generano e sostengono, o soggettano e diminuiscono, questa propensione innata. La teoria si focalizza su tre bisogni psicologici fondamentali:
• il bisogno di competenza,
• il bisogno di autonomia,
• il bisogno di relazionalità.
Il bisogno di competenza consiste nel desiderio di sentirsi in grado di agire sull’ambiente e di essere efficaci nel farlo. Fin dai primi studi sperimentali è stato osservato come i feedback di comportamenti positivi aumentassero la motivazione intrinseca, mentre quelli di performance negative la diminuissero (Deci, 1975), e come tutto ciò fosse mediato dalla
percezione delle proprie competenze (Vallard e Reid, 1984).
Il bisogno di autonomia riguarda la volontà di scegliere quale attività svolgere e come svilupparla. 
Il bisogno di relazionalità si riferisce alla necessità di mantenere e costituire legami in ambito sociale. Un clima di collaborazione in classe incentiva l’interesse allo studio in contrapposizione al voto, mentre ambienti con assetti competitivi portano ad un’inversione della tendenza. Si è in presenza di una situazione d'apprendimento ottimale quando tutti i tre bisogni psicologici fondamentali sono ugualmente soddisfatti.
E' fondamentale distinguere tra:
• comportamenti autodeterminati, ossia comportamenti completamente volontari che producono nel soggetto una conferma del proprio senso di sé (se il soggetto vive una
situazione di libera scelta aumenta o mantiene la motivazione per il compito)
• comportamenti controllati (se percepisce lo svolgimento di un’attività come imposto dall’esterno esso sarà meno autodeterminato).
L’assenza di motivazione è conseguenza della non valorizzazione di un’attività, di una sensazione di mancanza di competenze o di aspettative negative rispetto ai risultati desiderati. La motivazione estrinseca porta a svolgere un’attività
con il solo obiettivo di ottenere un premio o evitare una punizione. 
Invece l'identificazione porta all’accettazione del comportamento perché ritenuto importante, comporta un’identificazione da parte del soggetto nei valori nell’azione, avendo così un alto grado di autonomia e il soggetto integra nel
sé i valori e gli obiettivi esterni. L’approccio alle attività si ha perché queste vengono ritenute importanti e coerenti con i propri valori. Inoltre, lo scopo è di ottenere soddisfazione intrinseca che viene in genere associato ad interesse e divertimento. 
L’organismic integration theory
Creare un ambiente che favorisce la soddisfazione dei tre bisogni psicologici fondamentali può essere una buona strategia applicabile anche a contesti educativi.
Il bisogno di relazionalità
La prima ragione per cui un soggetto potrebbe essere disposto a svolgere un determinato compito è che questo sia valutato positivamente da persone considerate significative, a cui è, o vorrebbe, essere legato (famiglia, pari o società). Promuovendo un senso di appartenenza, obiettivi comuni o connessione a persone, gruppi o culture, l’individuo può provare un senso di relazionalità.
Il bisogno di competenza
Se non ci si sente capaci di svolgere una data attività difficilmente questa diviene significativa. Per supportare quest’ultima è necessario offrire sfide di livello adeguato agli studenti, con feedback significativi riguardo l’efficacia di ogni allievo.
Il bisogno di autonomia
Viene soddisfatto solo se si riesce a raggiungere la comprensione interiore del significato e del valore di un dato comportamento; se l’ambiente scolastico favorisce tale processo si renderà più agevole anche l’integrazione degli
obiettivi.

ATTEGGIAMENTO

La definizione semplice descrive l’atteggiamento come un grado di affettività positiva o negativa associato alla matematica; quella complessa vede il concetto suddiviso in tre dimensioni strettamente interconnesse tra loro:  
la disposizione e la risposta emozionale alla matematica, 
la visione e le convinzioni riguardanti la matematica, 
le competenze percepite e i comportamenti relativi alla matematica.

EMOZIONI

L’importanza delle emozioni era inizialmente relegata allo studio dell’ansia in matematica, che attingeva da teorie e metodi provenienti dall’ambito psicologico, collegata con l’ansia in generale, e da test con risultati bassi nella materia. L’interesse si è poi esteso ad una più ampia gamma di emozioni quando la ricerca è entrata in contatto con gli studi sul problem solving (McLeod e Adams, 1989), evidenziando l’importanza di aspetti come la speranza, la determinazione e le emozioni nei processi di risoluzione dei problemi.
McLeod, ad esempio, riteneva che i fattori affettivi fossero fortemente interconnessi ma ben distinti l’uno dall’altro: le reazioni emotive sembrano essere generate dall’atteggiamento verso la matematica, mentre le convinzioni dipendono dal contesto (culturale) e le esperienze individuali. McLeod individuò altri fattori che facevano parte della sfera dell’affect in didattica della matematica: 

• sicurezza,
• concetto di sé,
• autoefficacia,
• ansia matematica,

• attribuzioni casuali,
• impotenza appresa,
• autonomia,
• motivazione.

CONVINZIONI

Oggi si tende a dare importanza non solo a cosa una persona crede, ma anche a come crede: fortemente o debolmente, con passione o meno, cosciente o inconsapevole
delle ragioni che ne stanno alla base, ecc. Emerge così il focus sui sistemi di convinzioni, mediante cui si può descrivere come queste sono strutturate e organizzate.

ATTIVITA’

         ALLA SCOPERTA DEI PERCHE' NASCOSTI TRA PROCEDURE E SIGNIFICATI
                                
Il clima di laboratorio come contesto di apprendimento si rivela pertinente per favorire l’esplorazione e la scoperta, la formulazione di congetture e la ricerca di strategie adeguate ai problemi posti e alla ricerca delle soluzioni per incoraggiare l’apprendimento collaborativo e promuovere la consapevolezza del proprio modo di apprendere.
Possono configurarsi diverse tipologie di laboratori:

Laboratori tematici: per nuclei concettuali della matematica, che si sviluppino secondo strutture analoghe basate sui nuclei trasversali di processo relativi al porre e porsi problemi e all’argomentare e dimostrare.
Laboratori interdisciplinari: da coordinare in interazione con altre discipline scientifiche e dell’area linguistica e umanistica.
Laboratori transdisciplinari: progettazione comune di insegnanti di diverse discipline finalizzata all’integrazione nell’ottica di uno scenario per l’alunno che favorisca mobilitazione di competenze trasversali di problem solving e problem posing; in un’ottica di sviluppo e non solo di recupero di conoscenze e competenze. 
Laboratori per gruppi di livello, di interclasse o rivolti all’intera classe dove l’interazione sociale e l’integrazione di diversità di livelli, stili e comportamenti trovi terreno fertile, per il recupero, il rinforzo o lo sviluppo di competenze e conoscenze matematiche e trasversali. 

* Vengono coinvolte 2 Classi prime della Scuola Secondaria di secondo grado
* Ogni classe viene suddivisa in 2 sottogruppi di 10-13 studenti
* Proposte di attività di difficoltà adeguate e sufficientemente sfidanti rispetto alle competenze dello studente.
* Percorso articolato in 4 fasi: Assegnazione di un problema/esercizio; Presentazione di altri metodi (più lunghi o più veloci, etc...) per svolgere il problema/esercizio chiedendo agli studenti di tentare di spiegare il significato di quello che è stato fatto (essere un buon esecutore e avere il controllo delle operazioni); Confronto fra procedure diverse per ottenere lo stesso risultato e far emergere l'esigenza del perché; Rendere espliciti i perché delle diverse procedure mentre spesso essi rimangono nascosti per spostare il focus dalla procedura al significato, dal come al perché (Non ricordo se non capisco).

OBIETTIVI

* Corretta visione epistemologica della matematica
* Inclusione per scelta di metodologia più adatta 
* Percezione della libertà di scelta delle procedure (velocità o sicurezza?)
* Valutare la scelta più giusta a seconda del caso
* Sviluppo del senso di auto-efficacia
* Percezione delle proprie abilità
* Sviluppare la consapevolezza della differenza fra riuscire e capire

ANALISI

Non solo questionari chiusi
Di Martino (2011) asserisce che i questionari a risposta chiusa “obbligano” la persona a dover prendere posizione su aspetti considerati rilevanti dal ricercatore, ma non necessariamente dal soggetto, impedendo inoltre l’emergere di idee personali. Per indagare sui fattori affettivi mediante strumenti di self-report, è importante che questi diano la maggior libertà di espressione possibile, permettendo a chi scrive di prendere decisioni autonome su cosa sia importante dire e cosa no. L’analisi di queste decisioni può dare informazioni interessanti, come la centralità psicologica, collegamenti non logici e una dimensione temporale (Di Martino e Zan, 2011).
I testi narrativi
L’obiettivo del testo narrativo è quello di comprendere come gli studenti hanno interpretato l’esperienza di apprendimento della matematica e non di tentare l’improbabile compito di ricostruire fatti oggettivi. Siamo invece interessati a ciò che la persona pensa di aver fatto, ai motivi per cui pensa di averlo fatto, in quali tipi di situazione pensava di trovarsi e così via (Bruner).
Nelle analisi dei testi di tipo narrativo di solito non è richiesta una replicabilità dei risultati come criterio di validità, ma ogni decisione interpretativa deve essere adeguatamente giustificata.
I componenti che partecipano al processo sono almeno tre:
• il narratore, rappresentato dal testo;
• il theoretical framework, che fornisce i costrutti e gli strumenti per l'interpretazione;
• il monitoraggio riflessivo dell’atto della lettura e interpretazione, un autocontrollo dei processi decisionali che portano alle conclusioni sul materiale.
Di Martino e Zan (2010) utilizzano questa tecnica di indagine in uno studio teorico per la caratterizzazione del concetto di atteggiamento in matematica, basandosi sull’analisi di 2000 temi autobiografici dal titolo Io e la matematica.
Laboratori
Ciascuna tipologia, dovrebbe tendere a configurarsi, nel tempo, come pratica didattica ordinaria, quindi essere messe in opera anche nelle attività di classe in orario curriculare. L’insegnante ha un ruolo di progettista delle attività e di facilitatore durante la realizzazione delle stesse. Particolare attenzione nella fase progettuale deve essere riservata ad una innovazione delle pratiche di verifica e valutazione degli apprendimenti. Queste non possono ridursi a situazioni esplicite di attribuzione di giudizi o voti, ma devono assumere carattere di processo sistematico, non frammentario e locale, di validazione e valutazione delle conoscenze e dei saperi.